Time for another brain burner!
This puzzle is based on my game Tau (2011). TAU was evolved from another game of mine called OMEGA (2010) as a tool to help me teach my students how to multiply in binary base. It exploits a mechanic called ‘multiplicative scoring’.
Let’s start by drawing a square grid of any size (10×10, for example) and filling it with coins, one on each cell. This is our bitcoin field.

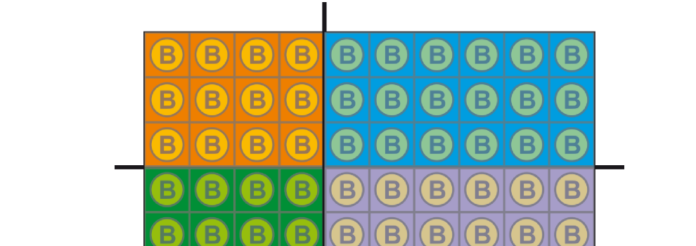
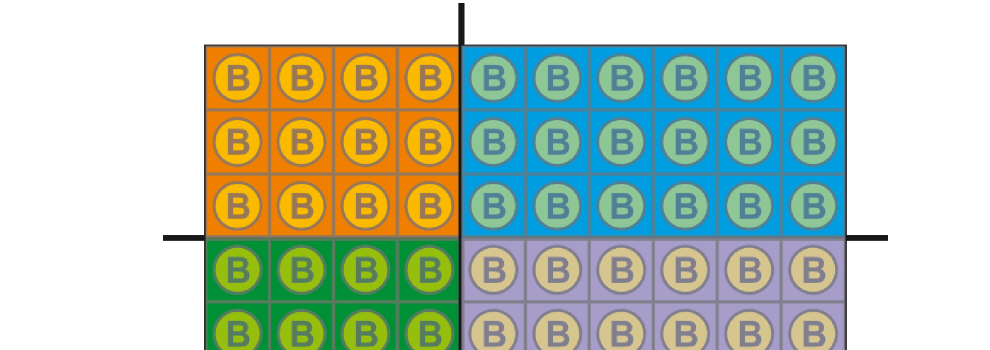
Now let’s split the field in two, by drawing a horizontal line like this:

Two groups of coins (above and below the line) have been created. In order to calculate our score, we multiply the number of coins of each group: S = 30 x 70 = 2.100 points.
Now let’s draw a vertical line like this:

Notice that now there are 4 groups. The new score is: S = 12 x 18 x 28 x 42 = 254.016.
By drawing this second line, we’ve managed to increase the score significantly. If we keep on drawing lines (creating groups) the score will keep on increasing for a while, but if we draw too many lines, it will start dropping!
In fact, if we draw all possible lines, the score will drop to 1 (100 groups of size 1 each)!

Notice also that drawing no lines produces a score of 100.
If a set of horizontal and/or vertical lines produces the highest possible score, this set is called a ‘solution’.
Challenge 1: Find a solution for a 10×10 field.
Challenge 2: Find a solution for a 1.000.000 x 1.000.000 field. Describe it instead of drawing it!
Let’s introduce an interesting twist now. What if some of the cells were empty?

Challenge 3: Find a solution for the field in figure 5. Empty groups have a value of zero!
And another twist: let’s mix bitcoins and dollars.

In this case, we define ‘solution’ as the partition that produces the highest possible bitcoin score and the lowest possible dollar score.
Challenge 4: Does a solution exist for the field in figure 6? If it does, can you find it?
Challenge 5: Find a partition for the field in figure 6 so that both the bitcoin and dollar scores are maximum.
Please post your answers in the comments section or here:
http://nestorgames.freeforums.org/bitcoin-magazine-puzzles-f16.html
… and I will reward the best post with a copy of one of my games. I’m looking forward to discussing your findings. Thank you for reading!